Das Rätsel der Zeit: Boltzmanns Entropie und der unscharfe Blick des menschlichen Beobachters

This text will be made available in English soon.

Dieser Text beinhaltet weiterführende Informationen zum Blogpost Das Rätsel der Zeit – Zeitfluss und Vergänglichkeit, der am 21.11.2024 auf dem Wissenschaftsblog „Natur des Glaubens“ von Michael Blume veröffentlicht wurde.

In diesem Text möchte ich den 2. Hauptsatz der Thermodynamik in der Interpretation von Ludwig Boltzmann – einem meiner ganz persönlichen Helden aus der Wissenschaft – mit einem einfachen Beispiel veranschaulichen und ein paar Betrachtungen hinzufügen. Die Thermodynamik eröffnet ein tieferes Verständnis unserer Erfahrung von Zeit: dass nichts bleibt wie es ist, dass Dinge immer in einer bestimmten Richtung ablaufen und sich irreversibel verändern.

Warum erleben wir die Zeit als unaufhaltsam voranschreitend?

Stellen Sie sich zwei Gefäße vor, die durch ein kleines Loch miteinander verbunden werden können. Anfänglich befindet sich eine Menge Gas nur im linken Gefäß. Sobald das Loch geöffnet wird, verteilt es sich auf beide Gefäße. Ohne äußere Einflüsse würde das Gas sich nie spontan wieder vollständig in einem der beiden Gefäße sammeln. (1)

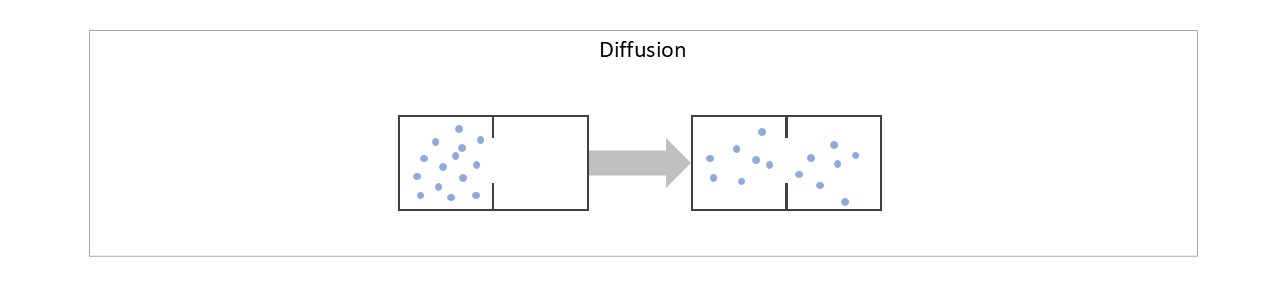
Gasmoleküle kann man sich annähernd wie winzige elastische Kugeln vorstellen, die aneinanderstoßen und voneinander abprallen, ähnlich wie beim Billard. Diese „ungeordnete“ Bewegung, die den Gesetzen der klassischen Mechanik folgt, ist die sogenannte thermische Bewegung, die wir als Wärme wahrnehmen. Für ein „ideales Gas“ (wie hier) wäre es theoretisch möglich, dass sich ein einmal ausgebreitetes Gas spontan in eines der Gefäße zurückzieht, ohne Energie zu verlieren. Doch warum passiert das nie?

Um das zu verstehen, müssen wir die Wahrscheinlichkeit der verschiedenen Anordnungen der Moleküle auf mikroskopischer Ebene – also auf der Größenskala der einzelnen Moleküle – betrachten. Man spricht hier auch von „Mikrozuständen“. Für eine große Anzahl von Molekülen gibt es nur sehr wenige Mikrozustände, in denen alle Moleküle im linken oder rechten Gefäß sind. Dagegen gibt es eine sehr große Anzahl von Mikrozuständen, in denen die Moleküle gleichmäßig auf beide Gefäße verteilt sind. Die Wahrscheinlichkeit, dass sich die Moleküle durch ungeordnete Bewegung alle links oder alle rechts sammeln, ist daher extrem gering. Den spontanen Eintritt in diesen Zustand beobachten wir in der Realität daher praktisch nie.

Wir schauen uns das an einem stark vereinfachten Modell an (nächstes Bild). Das Gas besteht hier aus nur drei Molekülen, und alle möglichen Verteilungen der Moleküle auf die beiden Gefäße sind eingezeichnet. Für drei Moleküle gibt es in diesem Szenario genau acht mögliche Mikrozustände. Von diesen acht Mikrozuständen gibt es jedoch nur zwei spezielle Zustände, in denen sich alle Moleküle in einem einzigen Gefäß befinden – links und rechts im Bild. Die verbleibenden sechs Mikrozustände in der Mitte repräsentieren Verteilungen, in denen die Moleküle auf beide Gefäße verteilt sind.

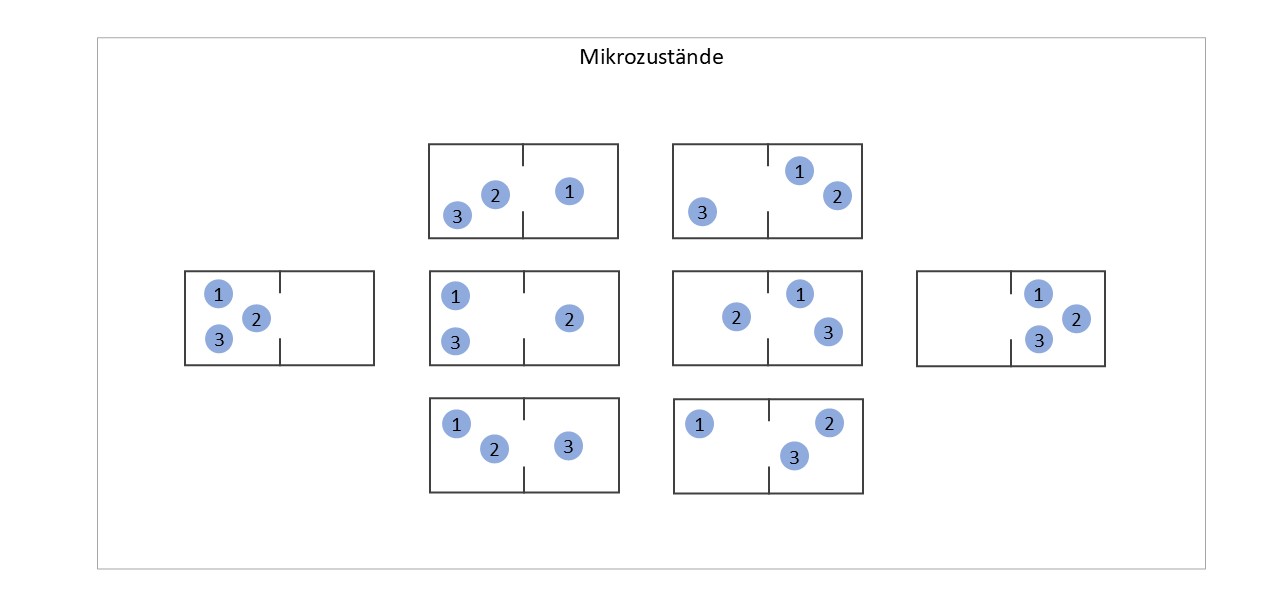
Schon in diesem sehr vereinfachten Modell ist es deutlich wahrscheinlicher, dass das Gas in einem der vielen Zustände vorliegt, in denen es auf beide Gefäße verteilt ist, als in einem der wenigen Zustände, in denen es sich vollständig auf ein Gefäß konzentriert.

Bei drei Molekülen ist der Effekt noch überschaubar. Doch für ein System mit N Molekülen gibt es für dieses Szenario insgesamt 2 hoch N mögliche Mikrozustände, und nur zwei dieser Zustände stellen die besondere Situation dar, in der sich das gesamte Gas in einem Gefäß konzentriert. Um das in einen greifbaren Kontext zu setzen: In einem „molaren Volumen“ von 22.4 Litern – im alltäglichen Maßstab – befinden sich etwa 6.022 × 10 hoch 23 Moleküle. Das entspricht etwa einer 6 mit 23 Nullen oder rund 600 Trilliarden. Man könnte poetisch sagen, dass es in einem Mol eines Gases ungefähr so viele Moleküle gibt wie Sterne im beobachtbaren Universum. (2)

Bei dieser enormen Zahl N von Molekülen ergibt sich eine unfassbar große Anzahl von Mikrozuständen. Damit ist die Wahrscheinlichkeit, dass alle Moleküle zufällig in nur einem der beiden Gefäße landen, verschwindend gering. Ein solcher Zustand tritt praktisch nie spontan auf und wird daher auch nie beobachtet. Dies erklärt der österreichische Physiker Ludwig Boltzmann als thermodynamische Grundlage des „Zeitpfeils“. Er führte die Entropie als Maß für die Anzahl der Mikrozustände ein, die einem bestimmten makroskopisch beobachtbaren Zustand entsprechen.

Auf Boltzmanns Grabstein in Wien ist die Formel für die Berechnung der Entropie aus der Anzahl der Mikrozustände eingraviert: (3)

S = k log W

Nach Boltzmann nimmt die Entropie in einem abgeschlossenen System stets zu. Auf mikroskopischer Ebene ist das gleichbedeutend mit: Ein System nimmt immer einen der wahrscheinlicheren Mikrozustände ein. Dies entspricht unserer alltäglichen Erfahrung, dass natürliche Prozesse bevorzugt in Richtung höherer Entropie verlaufen. Das ist der Zweite Hauptsatz der Thermodynamik.

Auf einer tieferen Ebene bietet Boltzmanns Entropie-Konzept eine physikalische Erklärung für die Prozesse, die wir Menschen als Vergänglichkeit und Verfall erleben.

Der Maxwellsche Dämon

Ein interessantes Gedankenexperiment in diesem Kontext stammt vom schottischen Physiker James Clerk Maxwell. Der „Maxwellsche Dämon“ ist ein hypothetisches Wesen, das die Bewegung einzelner Moleküle beobachten und gezielt darauf reagieren kann. Mit anderen Worten: Dieses Wesen wäre in der Lage, Mikrozustände direkt wahrzunehmen und so die Entropiezunahme zu verhindern. Im Beispiel der Gasexpansion könnte der Dämon auf mikroskopischer Ebene in das System eingreifen, indem er gezielt Moleküle so lenkt, dass sie sich alle in das linke Gefäß bewegen. Dadurch würde er das System in einen Zustand überführen, in dem die Entropie innerhalb dieses abgeschlossenen Systems nicht zunimmt, sondern abnimmt.

Das ursprüngliche Gedankenexperiment Maxwells bezog sich auf das Phänomen der spontanen Bewegung von Wärme in Richtung einer kälteren Region, für das aber ähnliche Überlegungen angestellt werden können. Dieses Gedankenexperiment kann dadurch aufgelöst werden, indem man den Begriff der Information einführt. Der hypothetische Dämon muss, um den Prozess auf mikroskopischer Ebene steuern und den „Zeitpfeil“ umkehren zu können, ständig Informationen sammeln und wieder löschen. Dies aber erfordert Energie und erzeugt wiederrum Entropie. In einem gewissen Sinne würde der Maxwellsche Dämon, wenn er es denn könnte, die Zeit umkehren. Das ist aber nicht möglich.

Mischungsentropie im Kaffee und der unscharfe Blick

Am Beispiel mit der Gasexpansion haben wir gesehen: Ein Mikrozustand, in dem alle Moleküle entweder im linken oder rechten Gefäß versammelt sind, wird von uns anders wahrgenommen als ein Mikrozustand, in dem das Gas gleichmäßig auf beide Behälter verteilt ist. Auf makroskopischer Ebene – also aus der Sicht eines menschlichen Beobachters – unterscheiden sich die Zustände mit den getrennten Gasen deutlich von denen, bei denen das Gas auf beide Gefäße verteilt ist.

Die Wahrscheinlichkeit eines makroskopischen Zustands hängt von der Anzahl der Mikrozustände ab, die ihn beschreiben: Je mehr Mikrozustände zu einem Makrozustand gehören, desto wahrscheinlicher erscheint er uns. Dies ist ein zentraler Punkt für das Verständnis der Entropie und für die Anwendung des zweiten Hauptsatzes der Thermodynamik. Alle Mikrozustände, in denen die Moleküle auf beide Gefäße verteilt sind, können wir makroskopisch nicht voneinander unterscheiden.

Ich möchte ein weiteres Beispiel geben.

Stellen Sie sich eine Tasse Kaffee vor. Wer einen Schuss Kaffeesahne hinzugibt, sieht, wie sich die Sahne (im Bild gelb) allmählich mit dem Kaffee (schwarz) mischt. Der umgekehrte Prozess – dass sich die Sahne wieder trennt – wird praktisch nie beobachtet. Dies ist ein Prozess, der nur in eine Richtung abläuft.

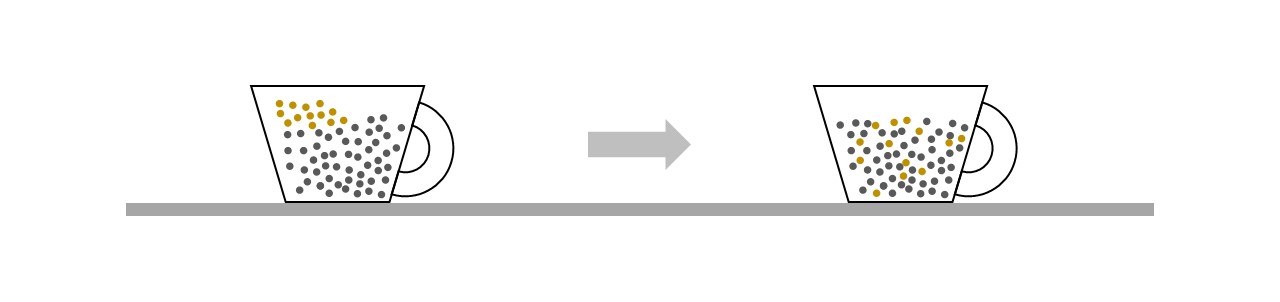
In Flüssigkeiten wie Sahne, die Lipide enthalten, treten allerdings Wechselwirkungen auf, die den Hang zur Vermischung teilweise bremsen. Um das Wesentliche an einem in der Zeit unumkehrbar voranschreitenden Prozesses zu verstehen, lassen Sie uns daher annehmen, dass sich die Teilchen im Kaffee wie in einem idealen Gas verhalten und derartige Wechselwirkungen ausgeschlossen sind. Vereinfachen wir weiter, so dass wir es nur mit 4 Teilchen zu tun haben: 2 Sahneteilchen (gelb) und 2 Kaffeeteilchen (schwarz). Es gibt 4!=24 mögliche Anordnungen für diese Teilchen.

Davon gibt es nur 4 Mikrozustände, in denen die Sahne in der oberen Hälfte versammelt ist.

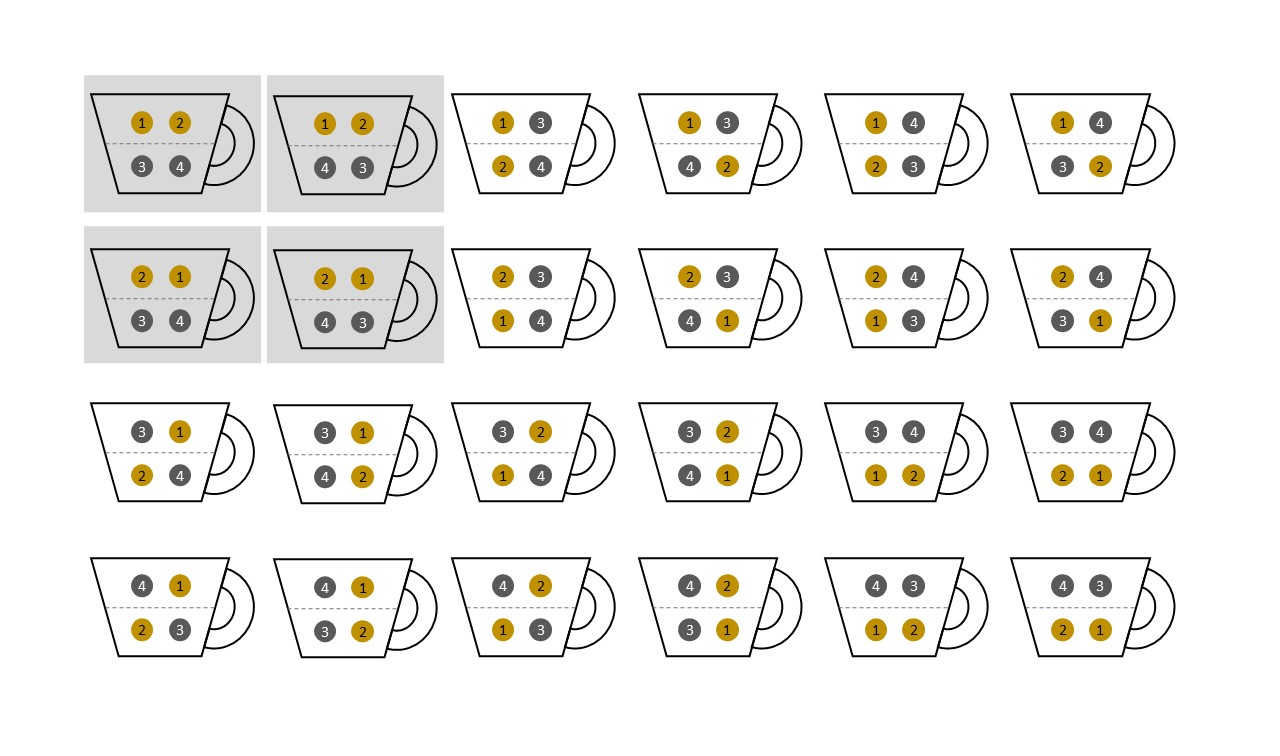
Die Entropie für den separierten Zustand ist geringer als die des durchmischten Zustandes, da die Anzahl der Mikrozustände im ersteren Fall viel geringer ist als im letzteren. Auch hier gilt: Im Alltag haben wir es mit einer unvorstellbar großen Anzahl von Teilchen zu tun, weshalb die Wahrscheinlichkeit für einen durchmischten Zustand im Vergleich zu einem entmischten Zustand extrem hoch ist. Diese Überlegungen führen letztlich zum Konzept der Mischungsentropie.

Betrachten wir aber nun den Fall, dass alle Teilchen identisch sind, also zum Beispiel nur aus Kaffeeteilchen bestehen. Wenn die Teilchen tatsächlich ununterscheidbar sind, zählen Permutationen derselben Teilchen nicht als unterschiedliche Mikrozustände. Makroskopisch gibt es also keinen Unterschied zwischen einem „gemischten“ und einem „separierten“ Zustand. Das bedeutet, dass hier keine Entropiezunahme beim Mischen auftreten kann. Genau dies ist der Kern des Gibbsschen Paradoxons. Es beschreibt die scheinbare Entropiezunahme bei der Mischung von zwei Gasen, selbst wenn die beiden Gase identisch sind. Die Entropiezunahme tritt nur auf, wenn man die Identität der Teilchen nicht korrekt berücksichtigt. Das Paradoxon wird durch die korrekte Berücksichtigung der Ununterscheidbarkeit der Teilchen gelöst. Im Falle identischer Gase, die gemischt werden, wird keine Entropiedifferenz gemessen, da die Teilchen ununterscheidbar sind.

Die Argumentation zum Zeitpfeil beruht darauf, dass wir Boltzmanns Definition der Entropie verwenden, die als Maß für die Anzahl der für makroskopische Beobachter ununterscheidbaren Mikrozustände dient. Wir können nicht wahrnehmen, wie sich einzelne Mikrozustände verändern, da wir keine „Maxwellschen Dämonen“ sind. Der Physiker Carlo Rovelli hat dafür den Begriff der „Unschärfe“ eingeführt:

„Diese Unschärfe steht im Zentrum von Boltzmanns Theorie. Aus der Unschärfe ergeben sich die Konzepte Wärme und Entropie, mit denen ihrerseits Phänomene verbunden sind, die den Fluss der Zeit auszeichnen. Insbesondere die Entropie eines Systems hängt explizit von der Unschärfe ab. Sie hängt ab von dem, was ich nicht sehe, weil sie von der Anzahl der ununterscheidbaren Konfigurationen abhängt. Ein und dieselbe mikroskopische Konfiguration kann mit Blick auf eine Unschärfe von hoher und mit Blick auf eine andere von geringer Entropie sein. Die Unschärfe ist ihrerseits kein geistiges Konstrukt: Sie hängt von der realen physikalischen Wechselwirkung ab, also hängt die Entropie von der physikalischen Wechselwirkung mit dem System ab.“ (Carlo Rovelli: „Die Ordnung der Zeit“, Rowohlt 2018, S. 121)

Warum gibt es komplexes Leben?

Lebewesen sind Gebilde mit einem hohen Mass an Organisation und Koordination, konkreter ausgedrückt: mit einer geordneten Anordnung und Funktion von Molekülen und Zellen. Unser Gehirn gehört vermutlich zu den komplexesten Strukturen, die wir kennen. Die Welt wird zwar durch Prozesse des Zerfalls und einer Tendenz zu zunehmender „Unordnung“ geprägt – doch wie passt dazu die Existenz von Leben?

Man könnte die obige Entropie-Diskussionen, die wir für relativ einfache Systeme geführt haben, auch auf den Vorgang anwenden, bei dem ein Ei auf den Boden fällt und zerspringt. Eine Analyse der Mikrozustände (die im Detail äußerst kompliziert ausfiele) würde zeigen, warum ein einmal zersprungenes Ei sich praktisch nie spontan wieder zu einem intakten Ei zusammensetzt. Denn es ist plausibel, dass die Anzahl der Mikrozustände im Zustand des zersprungenen Eies extrem viel größer ist als im intakten Zustand. Dies macht den Prozess des Zerspringens irreversibel.

Dennoch hat sich auf der Erde hochkomplexes Leben entwickelt. Wie konnte sich etwas so Geordnetes und Komplexes wie der Mensch im Lauf der Evolution bilden, wenn die Tendenz doch zur Unordnung geht? Offensichtlich hat ein Mensch im Vergleich zu einer ungeordneten Anordnung der gleichen Moleküle eine hohe Organisation und damit eine relativ niedrige Entropie.

Die Antwort liegt darin, dass das Leben auf der Erde fernab vom thermodynamischen Gleichgewicht existiert. Unsere Biosphäre ist ein offenes System, das Energie aus seiner Umgebung – insbesondere von der Sonne – aufnimmt. Diese Energie ermöglicht es Lebewesen, lokal Ordnung zu schaffen und ihre eigene Struktur aufrechtzuerhalten, indem sie Entropie in die Umgebung exportieren (beispielsweise durch die Abgabe von Wärme oder die Produktion hoch-entropischer Stoffwechselprodukte), das heißt durch einen Prozess der Externalisierung.

Oder, wie der Physiker Erwin Schrödinger (4) schreibt:

„… das Wesentliche am Stoffwechsel ist, dass es dem Organismus gelingt, sich von der Entropie zu befreien, die er, solange er lebt, erzeugen muss.“

Während Lebewesen durch Stoffwechselprozesse ihre Organisation erhalten, steigt die Entropie des gesamten Systems – Erde und Sonnenstrahlung – kontinuierlich an.

Auf diese Weise ist es für Lebewesen, einschließlich uns Menschen, möglich, ihre eigene Entropie vorübergehend – für die Zeit ihrer Lebensspanne – zu verringern und dem Zerfall, der mit einer Entropiezunahme einhergeht, zu entkommen.

Der Physiker Roger Penrose (5) erklärt es so:

„Die Erde gibt die gleiche Energiemenge zurück, die sie von der Sonne erhält, aber das, was sie von der Sonne empfängt, ist in einer viel niedrigeren Entropieform, da das gelbe Sonnenlicht eine höhere Frequenz hat als das Infrarotlicht, das die Erde zurückstrahlt. Dementsprechend tragen die Photonen der Sonne (…) mehr Energie pro Photon als diejenigen, die die Erde zurückgibt, sodass die Energie von der Sonne von weniger Photonen getragen wird als die von der Erde zurückgegebene. Weniger Photonen bedeuten weniger Freiheitsgrade und damit einen kleineren Phasenraumbereich und damit eine geringere Entropie als bei den in den Weltraum zurückgeführten Photonen. Pflanzen nutzen diese Energie geringer Entropie bei der Photosynthese und reduzieren dadurch ihre eigene Entropie. Wir nutzen Pflanzen, um unsere zu reduzieren, indem wir sie essen oder etwas essen, das sie frisst, und indem wir den Sauerstoff einatmen, den die Pflanzen freisetzen. Dies ist letztlich auf das Temperaturungleichgewicht am Himmel zurückzuführen, das aus der gravitativen Verklumpung resultiert, die die Sonne hervorgebracht hat.“